01
de 05
Números babilónicos
Tres áreas principales de diferencia de nuestros números
Número de símbolos utilizados en la matemática babilónica
Imagínese lo fácil que sería aprender aritmética en los primeros años si todo lo que tuviera que hacer fuera aprender a escribir una línea como yo y un triángulo. Eso es básicamente todo lo que los pueblos antiguos de Mesopotamia tenían que hacer, aunque los variaban aquí y allá, alargándose, girando, etc.
No tenían nuestros bolígrafos y lápices, ni papel para el caso. Lo que escribieron fue una herramienta que uno usaría en la escultura, ya que el medio era arcilla. Si esto es más difícil o más fácil de aprender que manejar con un lápiz es una sacudida, pero hasta ahora están por delante en el departamento de facilidad, con solo dos símbolos básicos para aprender.
Base 60
El siguiente paso arroja una llave en el departamento de simplicidad. Usamos un Base 10, un concepto que parece obvio ya que tenemos 10 dígitos. De hecho, tenemos 20, pero supongamos que usamos sandalias con cubiertas protectoras para los pies para evitar la arena el desierto, caliente por el mismo sol que hornearía las tabletas de arcilla y las preservaría para que podamos encontrar milenios luego. Los babilonios usaron esta Base 10, pero solo en parte. En parte, usaron la Base 60, el mismo número que vemos a nuestro alrededor en minutos, segundos y grados de un triángulo o círculo. Eran astrónomos consumados, por lo que el número podría provenir de sus observaciones de los cielos. Base 60 también tiene varios factores útiles que facilitan el cálculo. Aún así, tener que aprender Base 60 es intimidante.
En "Homenaje a Babilonia" [La Gaceta MatemáticaVol. 76, N ° 475, "El uso de la historia de las matemáticas en la enseñanza de las matemáticas" (marzo de 1992), págs. 158-178], el escritor y maestro Nick Mackinnon dice que usa las matemáticas babilónicas para enseñar a los niños de 13 años sobre bases distintas de 10. El sistema babilónico utiliza la base 60, lo que significa que en lugar de ser decimal, es sexagesimal.
Notación posicional
Tanto el sistema de numeración babilónico como el nuestro dependen de la posición para dar valor. Los dos sistemas lo hacen de manera diferente, en parte porque su sistema carecía de un cero. Aprender el sistema posicional babilónico de izquierda a derecha (de mayor a menor) para probar por primera vez la aritmética básica probablemente ya no exista. difícil que aprender nuestro 2-direccional, donde tenemos que recordar el orden de los números decimales, aumentando desde el decimal, unos, decenas, cientos y luego desplegándose en la otra dirección en el otro lado, sin columna de un solo décimo, centésimo, milésimas, etc.
Iré a las posiciones del sistema babilónico en más páginas, pero primero hay algunas palabras numéricas importantes que aprender.
Años babilónicos
Hablamos de períodos de años usando cantidades decimales. Tenemos una década por 10 años, un siglo por 100 años (10 décadas) o 10X10 = 10 años al cuadrado, y un milenio por 1000 años (10 siglos) o 10X100 = 10 años en cubos. No conozco ningún término más alto que ese, pero esas no son las unidades que usaban los babilonios. Nick Mackinnon se refiere a una tableta de Senkareh (Larsa) de Sir Henry Rawlinson (1810-1895) * para las unidades que usaron los babilonios y no solo por los años involucrados sino también las cantidades implicadas:
- soss
- ner
- sar.
sossnersosssarsoss
Todavía no hay desempate: no es necesariamente más fácil aprender los términos de años cuadrados y cubicos derivados del latín de lo que son babilonios de una sílaba que no implican cubos, sino multiplicación por 10.
¿Qué piensas? ¿Habría sido más difícil aprender los conceptos básicos de números como un niño de la escuela de Babilonia o como un estudiante moderno en una escuela de habla inglesa?
* George Rawlinson (1812-1902), hermano de Henry, muestra una tabla de cuadrados transcrita simplificada en Las siete grandes monarquías del antiguo mundo oriental. La tabla parece ser astronómica, basada en las categorías de los años babilónicos.
Todas las fotos provienen de esta versión escaneada en línea de una edición del siglo XIX de George Rawlinson Las siete grandes monarquías del mundo oriental antiguo.02
de 05
Los números de las matemáticas babilónicas
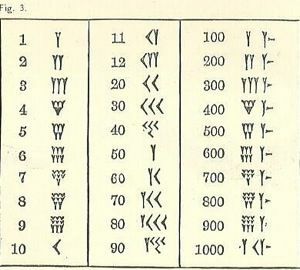
Como crecimos con un sistema diferente, los números babilónicos son confusos.
Al menos los números van de alto a la izquierda a bajo a la derecha, como nuestro sistema árabe, pero el resto probablemente parezca desconocido. El símbolo de uno es una forma de cuña o en forma de Y. Desafortunadamente, la Y también representa un 50. Hay algunos símbolos separados (todos basados en la cuña y la línea), pero todos los demás números se forman a partir de ellos.
Recuerda que la forma de escribir es cuneiforme o en forma de cuña. Debido a la herramienta utilizada para dibujar las líneas, hay una variedad limitada. La cuña puede o no tener una cola, dibujada tirando del lápiz de escritura cuneiforme a lo largo de la arcilla después de imprimir la forma del triángulo parcial.
El 10, descrito como una punta de flecha, se parece un poco a
Tres filas de hasta 3 pequeños 1s (escritos como Ys con algunas colas acortadas) o 10s (un 10 se escribe como
03
de 05
1 fila, 2 filas y 3 filas
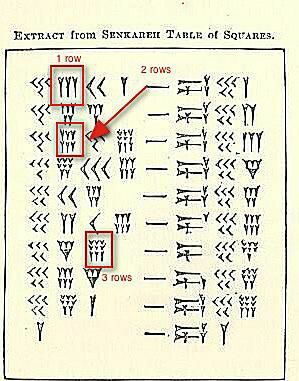
Hay tres conjuntos de números cuneiformes. racimos resaltado en la ilustración de arriba.
En este momento, no estamos interesados en su valor, sino en demostrar cómo vería (o escribiría) en cualquier lugar del 4 al 9 del mismo número agrupado. Tres van seguidos. Si hay un cuarto, quinto o sexto, va por debajo. Si hay una séptima, octava o novena, necesita una tercera fila.
Las siguientes páginas continúan con instrucciones sobre cómo realizar cálculos con la cuneiforme babilónica.
04
de 05
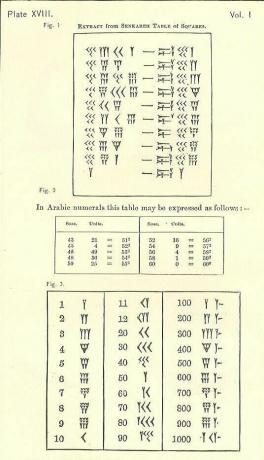
La tabla de cuadrados
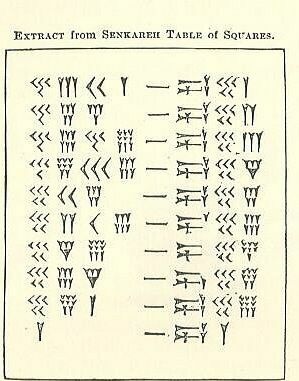
De lo que has leído arriba sobre el soss - lo que recordará es el babilónico durante 60 años, la cuña y la punta de flecha - que son nombres descriptivos para las marcas cuneiformes, vea si puede descubrir cómo funcionan estos cálculos. Un lado de la marca de guión es el número y el otro es el cuadrado. Pruébalo en grupo. Si no puede resolverlo, mire el siguiente paso.
05
de 05
Cómo decodificar la tabla de cuadrados

¿Puedes resolverlo ahora? Dame una oportunidad.
...
Hay 4 columnas claras en el lado izquierdo seguidas por un signo de guión y 3 columnas a la derecha. Mirando el lado izquierdo, el equivalente de la columna 1s es en realidad las 2 columnas más cercanas al "guión" (columnas internas). Las otras 2 columnas externas se cuentan juntas como la columna de los 60.
- El 4-
- Las 3 Ys = 3.
- 40+3=43.
- El único problema aquí es que hay otro número después de ellos. Esto significa que no son unidades (el lugar de las unidades). El 43 no es 43, sino 43-60, ya que es el sistema sexagesimal (base 60) y está en el soss columna como lo indica la tabla inferior.
- Multiplica 43 por 60 para obtener 2580.
- Agregue el siguiente número (2-
- Ahora tienes 2601.
- Ese es el cuadrado de 51.
La siguiente fila tiene 45 en el soss columna, entonces multiplica 45 por 60 (o 2700), y luego agrega el 4 de la columna de unidades, entonces tienes 2704. La raíz cuadrada de 2704 es 52.
¿Puedes entender por qué el último número = 3600 (60 al cuadrado)? Sugerencia: ¿Por qué no es 3000?